Resolução do exercício de matemática:
1.
No contexto do problema, tanto o tempo como a altura têm que ser não negativos.
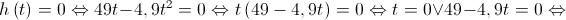
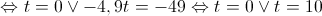
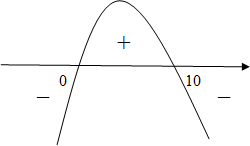
Logo, ![t \in \left[ {0,10} \right] t \in \left[ {0,10} \right]](/images/jlatex/b9cf6f11e8a27b37a32630f31f36e76a.gif)
2.
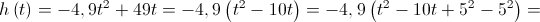
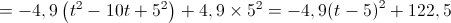
Logo, as coordenadas do vértice da parábola, imagem geométrica da função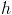 são:
são: 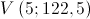
Logo, a altura máxima atingida pela bola é de 122,5 m.
3.
Sabe-se que:
- Coordenadas do vértice:
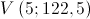
- Parábola com a concavidade voltada para baixo
Logo, a função é estritamente crescente no intervalo![\left[ {0,5} \right] \left[ {0,5} \right]](/images/jlatex/4e06417389c57bb84fba729031f5da0f.gif) .
.
Logo, a bola subiu durante os primeiros 5 segundos.

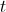 segundos é dada pela expressão
segundos é dada pela expressão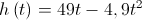 .
.
