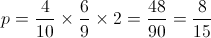Solução do Exercício:
1.
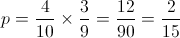
2.

Uma caixa contém 10 bolas numeradas de 1 a 10, sendo as 4 primeiras azuis e as seis últimas vermelhas.
Retiram-se, sucessivamente e sem reposição duas bolas da caixa.
1. Determine a probabilidade de sairem duas bolas azuis.
2. Determine a probabilidade de sairem duas bolas de cor diferente.
1.
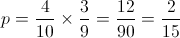
2.