Resolução do exercício de matemática:
1.
Estude a função  quanto à existência de assíntotas não verticais do seu gráfico.
quanto à existência de assíntotas não verticais do seu gráfico.
Resolução:
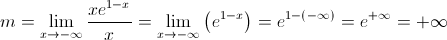
Logo, não existem assíntotas horizontais nem oblíquas quando 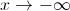 .
.
Vamos ver o que acontece quando 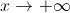 .
.
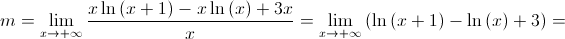
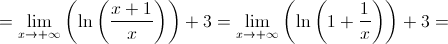
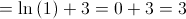
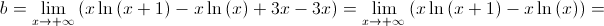
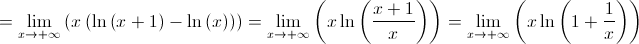
Mudança de variável: 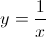 ; quando
; quando 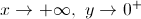 .
.
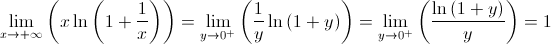
Logo, 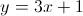 é a equação da única assíntota não vertical do gráfico de
é a equação da única assíntota não vertical do gráfico de  .
.
2.
Para 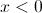 , tem-se:
, tem-se:
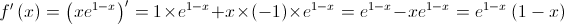
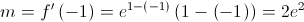
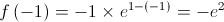
coordenadas do ponto de tangência: 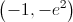
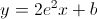
Substituindo pelas coordenadas do ponto de tangência, vem:
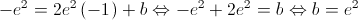
equação da reta tangente no ponto de abcissa -1: 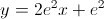
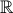 , definida por:
, definida por: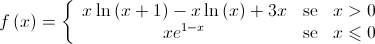
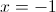 .
.