Exercicios de Matematica 10º Ano | Estatística | Exercicio 2

Exercicios de Matematica 10º Ano

Estatística

Exercício 2

As idades dos jogadores de futebol de uma equipa são as seguintes:

27, 30, 22, 26, 26, 30, 28, 29, 30, 22, 29

1. Calcule a média. Apresente o resultado com uma casa decimal.

2. Calcule o desvio padrão. Apresente o resultado com uma casa decimal.

3. Indique a moda.

4. Determine os quartis e amplitude inter-quartil.

Resolução dos exercícios de matemática:

1. Vamos organizar os dados numa tabela

Idade	Frequência Absoluta
22	2
26	2
27	1
28	1
29	2
30	3

Cálculo da média:

$\overline x = \frac{{22 \times 2 + 26 \times 2 + 27 \times 1 + 28 \times 1 + 29 \times 2 + 30 \times 3}}{{11}} =$

$= \frac{{299}}{{11}} = 27,2$

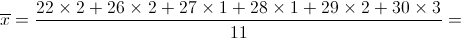
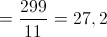
2. Cálculo do desvio padrão

$= \frac{{87,64}}{{11}} = \frac{{2191}}{{275}}$

$\sigma = \sqrt {\frac{{2191}}{{275}}} \simeq 2,8$

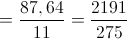
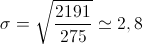
3. A moda é o valor mais frequente, logo, a moda é 30.

4. Na estatística, um quartil é qualquer um dos três valores que divide o conjunto ordenado de dados em quatro partes iguais, e assim cada parte representa 1/4 da amostra ou população.

Assim, para determinar os quartis vamos colocar os dados por ordem crescente:

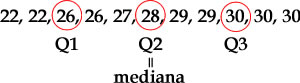
calculo-dos-quartis

primeiro quartil (designado por Q1/4) = quartil inferior = é o valor aos 25% da amostra ordenada = 25º percentil

segundo quartil (designado por Q2/4) = mediana = é o valor até ao qual se encontra 50% da amostra ordenada = 50º percentil, ou 5º decil.

terceiro quartil (designado por Q3/4) = quartil superior = valor a partir do qual se encontram 25% dos valores mais elevados = valor aos 75% da amostra ordenada = 75º percentil

À diferença entre os quartis superior e inferior chama-se amplitude inter-quartil.

Amplitude inter-quartil = 30 - 26 = 4

Atividades Relacionadas

Exercicios de Matematica 10º Ano | Estatística | Exercicio 1 →