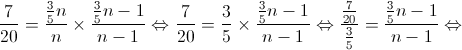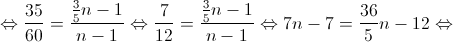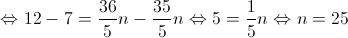Resolução do exercício de matemática:
1. Sejam:
A: “a bola é preta”
B: “a bola tem um número ímpar”
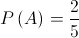
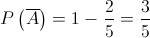
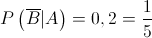
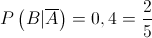
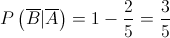
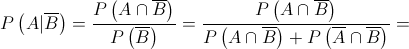
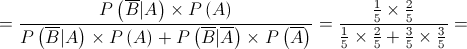
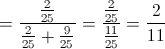
2. Das 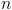 bolas que a caixa contém
bolas que a caixa contém 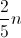 são pretas e
são pretas e 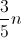 são brancas.
são brancas.
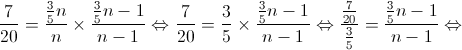
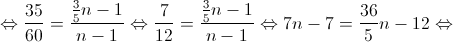
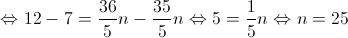
Uma caixa contém apenas bolas brancas e bolas pretas, indistinguíveis ao tato.
Todas as bolas estão numeradas com um único número natural.
Sabe-se que:
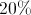 das bolas pretas têm um número par;
das bolas pretas têm um número par;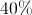 das bolas brancas têm um número ímpar.
das bolas brancas têm um número ímpar.
1. Retira-se, ao acaso, uma bola dessa caixa.
Determine a probabilidade de essa bola ser preta, sabendo que tem um número par.
Apresente o resultado na forma de fração irredutível.
2. Admita agora que a caixa tem 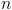 bolas.
bolas.
Extraem-se, ao acaso, sucessivamente e sem reposição, duas bolas da caixa.
Determine 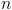 , sabendo que a probabilidade de ambas as bolas serem brancas é igual a
, sabendo que a probabilidade de ambas as bolas serem brancas é igual a 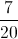 .
.
Resolução do exercício de matemática:
1. Sejam:
A: “a bola é preta”
B: “a bola tem um número ímpar”
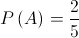
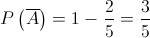
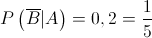
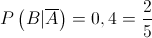
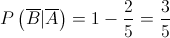
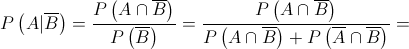
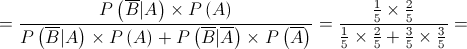
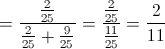
2. Das 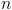 bolas que a caixa contém
bolas que a caixa contém 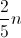 são pretas e
são pretas e 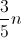 são brancas.
são brancas.