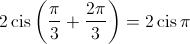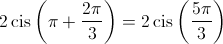Resolução do exercício de Matemática:
4.1. 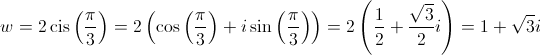
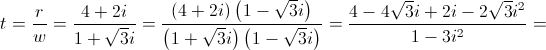
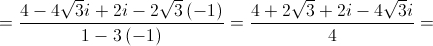
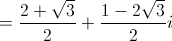
4.2. 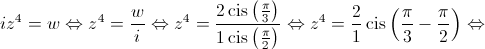
![\Leftrightarrow {z^4} = 2\operatorname{cis} \left( { - \frac{\pi }{6}} \right) \Leftrightarrow z = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{ - \frac{\pi }{6} + 2k\pi }}{4}} \right),k \in \left\{ {0,1,2,3} \right\} \Leftrightarrow \Leftrightarrow {z^4} = 2\operatorname{cis} \left( { - \frac{\pi }{6}} \right) \Leftrightarrow z = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{ - \frac{\pi }{6} + 2k\pi }}{4}} \right),k \in \left\{ {0,1,2,3} \right\} \Leftrightarrow](/images/jlatex/690de62896d5d97383600b8ab593416e.gif)
![\Leftrightarrow z = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{{k\pi }}{2}} \right),k \in \left\{ {0,1,2,3} \right\} \Leftrightarrow z = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{{k\pi }}{2}} \right),k \in \left\{ {0,1,2,3} \right\}](/images/jlatex/f00ae2e4eb532b3a81178e6bebcc5ef0.gif)
![k = 0,{\text{ }}{z_1} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}}} \right) k = 0,{\text{ }}{z_1} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}}} \right)](/images/jlatex/e6c8f0f814ffc1202f0113702bdec842.gif)
![k = 1,{\text{ }}{z_2} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{\pi }{2}} \right) = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{11\pi }}{{24}}} \right) k = 1,{\text{ }}{z_2} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{\pi }{2}} \right) = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{11\pi }}{{24}}} \right)](/images/jlatex/6026882bb50d42c5f06fd6aa8f11ff63.gif)
![k = 2,{\text{ }}{z_2} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{{2\pi }}{2}} \right) = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{23\pi }}{{24}}} \right) k = 2,{\text{ }}{z_2} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{{2\pi }}{2}} \right) = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{23\pi }}{{24}}} \right)](/images/jlatex/636fca39a339016b815b2a5b0d45281b.gif)
![k = 3,{\text{ }}{z_2} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{{3\pi }}{2}} \right) = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{35\pi }}{{24}}} \right) k = 3,{\text{ }}{z_2} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{{3\pi }}{2}} \right) = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{35\pi }}{{24}}} \right)](/images/jlatex/751bd50854d01fde3be47400898df2f5.gif)
![S = \left\{ {\sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}}} \right),\sqrt[4]{2}\operatorname{cis} \left( {\frac{{11\pi }}{{24}}} \right),\sqrt[4]{2}\operatorname{cis} \left( {\frac{{23\pi }}{{24}}} \right),\sqrt[4]{2}\operatorname{cis} \left( {\frac{{35\pi }}{{24}}} \right)} \right\} S = \left\{ {\sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}}} \right),\sqrt[4]{2}\operatorname{cis} \left( {\frac{{11\pi }}{{24}}} \right),\sqrt[4]{2}\operatorname{cis} \left( {\frac{{23\pi }}{{24}}} \right),\sqrt[4]{2}\operatorname{cis} \left( {\frac{{35\pi }}{{24}}} \right)} \right\}](/images/jlatex/3b6d5adcf679234e9af6559ad7c3a0f8.gif)
4.3. 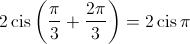
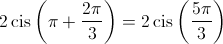
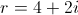 e
e 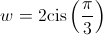 .
.
4.1. Represente na forma algébrica o complexo 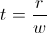 .
.
4.2. Resolva, em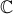 , a equação
, a equação 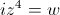 .
.
4.3. Sabe-se que 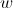 é uma das raízes cúbicas de um complexo
é uma das raízes cúbicas de um complexo 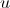 , determine as outras raízes cúbicas de
, determine as outras raízes cúbicas de 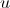 .
.
Resolução do exercício de Matemática:
4.1. 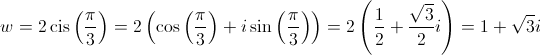
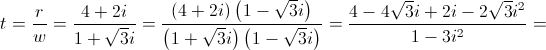
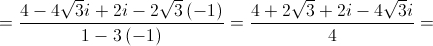
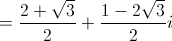
4.2. 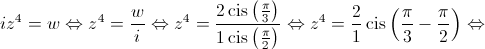
![\Leftrightarrow {z^4} = 2\operatorname{cis} \left( { - \frac{\pi }{6}} \right) \Leftrightarrow z = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{ - \frac{\pi }{6} + 2k\pi }}{4}} \right),k \in \left\{ {0,1,2,3} \right\} \Leftrightarrow \Leftrightarrow {z^4} = 2\operatorname{cis} \left( { - \frac{\pi }{6}} \right) \Leftrightarrow z = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{ - \frac{\pi }{6} + 2k\pi }}{4}} \right),k \in \left\{ {0,1,2,3} \right\} \Leftrightarrow](/images/jlatex/690de62896d5d97383600b8ab593416e.gif)
![\Leftrightarrow z = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{{k\pi }}{2}} \right),k \in \left\{ {0,1,2,3} \right\} \Leftrightarrow z = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{{k\pi }}{2}} \right),k \in \left\{ {0,1,2,3} \right\}](/images/jlatex/f00ae2e4eb532b3a81178e6bebcc5ef0.gif)
![k = 0,{\text{ }}{z_1} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}}} \right) k = 0,{\text{ }}{z_1} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}}} \right)](/images/jlatex/e6c8f0f814ffc1202f0113702bdec842.gif)
![k = 1,{\text{ }}{z_2} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{\pi }{2}} \right) = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{11\pi }}{{24}}} \right) k = 1,{\text{ }}{z_2} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{\pi }{2}} \right) = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{11\pi }}{{24}}} \right)](/images/jlatex/6026882bb50d42c5f06fd6aa8f11ff63.gif)
![k = 2,{\text{ }}{z_2} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{{2\pi }}{2}} \right) = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{23\pi }}{{24}}} \right) k = 2,{\text{ }}{z_2} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{{2\pi }}{2}} \right) = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{23\pi }}{{24}}} \right)](/images/jlatex/636fca39a339016b815b2a5b0d45281b.gif)
![k = 3,{\text{ }}{z_2} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{{3\pi }}{2}} \right) = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{35\pi }}{{24}}} \right) k = 3,{\text{ }}{z_2} = \sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}} + \frac{{3\pi }}{2}} \right) = \sqrt[4]{2}\operatorname{cis} \left( {\frac{{35\pi }}{{24}}} \right)](/images/jlatex/751bd50854d01fde3be47400898df2f5.gif)
![S = \left\{ {\sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}}} \right),\sqrt[4]{2}\operatorname{cis} \left( {\frac{{11\pi }}{{24}}} \right),\sqrt[4]{2}\operatorname{cis} \left( {\frac{{23\pi }}{{24}}} \right),\sqrt[4]{2}\operatorname{cis} \left( {\frac{{35\pi }}{{24}}} \right)} \right\} S = \left\{ {\sqrt[4]{2}\operatorname{cis} \left( { - \frac{\pi }{{24}}} \right),\sqrt[4]{2}\operatorname{cis} \left( {\frac{{11\pi }}{{24}}} \right),\sqrt[4]{2}\operatorname{cis} \left( {\frac{{23\pi }}{{24}}} \right),\sqrt[4]{2}\operatorname{cis} \left( {\frac{{35\pi }}{{24}}} \right)} \right\}](/images/jlatex/3b6d5adcf679234e9af6559ad7c3a0f8.gif)
4.3.