Resolução dos exercícios de matemática:
1.1. 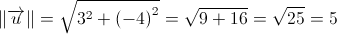
1.2. O simétrico de 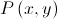 em relação à bissectriz dos quadrantes ímpares é
em relação à bissectriz dos quadrantes ímpares é 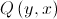 . Logo,
. Logo, 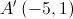 .
.
1.3. Um vetor diretor da reta é: 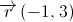
Logo, 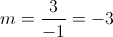 .
.
Logo, a equação reduzida da reta é do tipo: 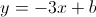 .
.
Como 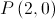 é um ponto da reta
é um ponto da reta 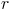 , tem-se que:
, tem-se que:
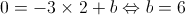
Logo, a equação reduzida da reta 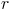 é:
é: 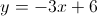 .
.
1.4. Como as retas 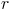 e
e 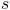 são paralelas, têm o mesmo declive
são paralelas, têm o mesmo declive 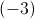 .
.
Logo, a equação reduzida da reta é do tipo: 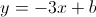 .
.
Como 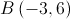 é um ponto da reta
é um ponto da reta 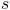 , tem-se que:
, tem-se que:
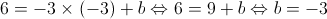
Logo, a equação reduzida da reta 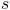 é:
é: 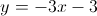 .
.

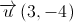 e
e 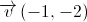 ; os pontos
; os pontos 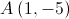 e
e 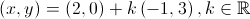 .
.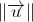 .
.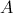 em relação à bissetriz dos quadrantes ímpares.
em relação à bissetriz dos quadrantes ímpares.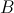 .
.