A intensidade de um som relaciona-se com a amplitude da onda sonora.
Considera-se que o nível sonoro, N, medido em decibéis (dB), é função da intensidade sonora, I, medida em watt por metro quadrado (W/m²), de acordo com a igualdade
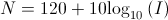 para
para 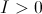
2.1. A legislação portuguesa estipula que, para veículos motorizados de duas rodas de de cilindrada, o nível sonoro
desses veículos, quando em funcionamento, não deve exceder o limite máximo de 105 dB.
Determine o valor da intensidade sonora, em W/m², que corresponde ao limite de 105 dB.
Apresente o resultado arredondado às centésimas.
2.2. O Rui fez um trabalho escolar em que relacionou a intensidade sonora com o nível sonoro.
Nesse trabalho, incluiu uma tabela que continha, para diferentes tipos de fontes sonoras, as respetivas intensidades,
em W/m², e os respetivos níveis sonoros em dB.
Apresenta-se, a seguir, parte dessa tabela.
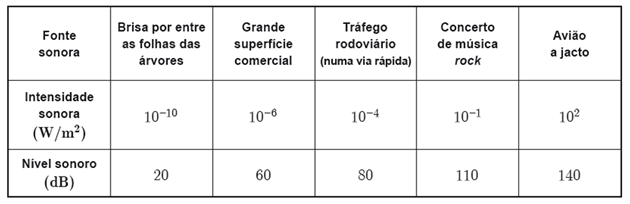
O texto seguinte é um excerto do trabalho elaborado pelo Rui.
«De acordo com o modelo que relaciona o nível sonoro com a intensidade sonora, podemos concluir que:
I) o nível sonoro de 0 decibéis, que marca o limiar inferior da audição humana, corresponde a uma intensidade de 0,000 000 000 01 W/m²;
II) ao compararmos o nível sonoro provocado pela sirene de um navio, cuja intensidade é cerca de 5 W/m², com os níveis sonoros mais elevados que constam da tabela, verificamos que esse nível sonoro está mais próximo do nível sonoro registado no concerto de música rock do que do nível sonoro registado no funcionamento do avião a jacto;
III) a intensidade sonora do avião a jacto em funcionamento é cerca de 600 vezes superior à intensidade sonora causada pelo tráfego rodoviário que circula numa via rápida.»
As conclusões I), II) e III) formuladas pelo Rui são todas incorretas.
Elabore uma pequena composição na qual, para cada uma das conclusões formuladas pelo Rui, apresente uma razão que fundamente a respetiva incorreção.
Exercicios de Matematica 12 ANO - Função logarítmica - Exercício 2→
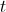 segundos é dada pela expressão
segundos é dada pela expressão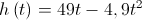 .
.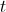 ?
?
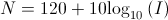 para
para 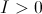

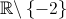 , definida por
, definida por 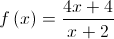 .
.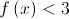 .
. .
.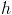 definida por
definida por 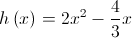 .
.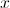 de tais que
de tais que 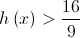 .
.