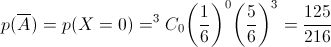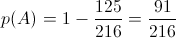Resolução do Problema:
1.
O dado tem 6 faces; uma delas tem o número 5. Logo,
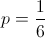
2.
A variável X: " nº de vezes que sai a face com o número 4" tem distribuição binomial de parâmetros 3 e  .
.
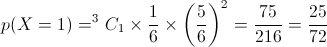
3.
A variável X: " nº de vezes que sai a face com o número 3" tem distribuição binomial de parâmetros 3 e  .
.
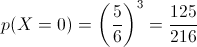
4.
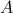 :"Obter pelo menos uma vez a face com o número 1" é o acontecimento contrário do acontecimento
:"Obter pelo menos uma vez a face com o número 1" é o acontecimento contrário do acontecimento
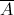 :"Não sair nenhuma vez a face com o número 1"
:"Não sair nenhuma vez a face com o número 1"
A variável X: " nº de vezes que sai a face com o número 1" tem distribuição binomial de parâmetros 3 e  .
.