Resolução do exercício de matemática:
1.
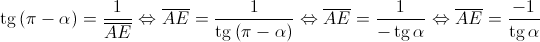
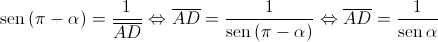
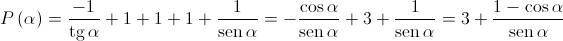
2.
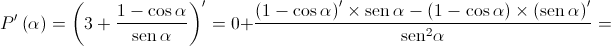
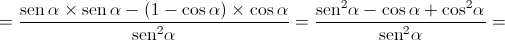
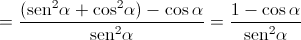
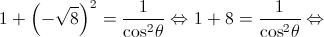
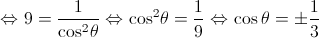
Como ![\theta \in \left] {\frac{\pi }{2},\pi } \right[ \theta \in \left] {\frac{\pi }{2},\pi } \right[](/images/jlatex/d52539df7bc27f4d4b002f62c4b61626.gif) , vem que
, vem que 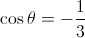 .
.
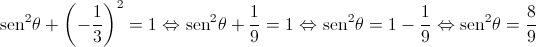
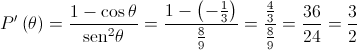
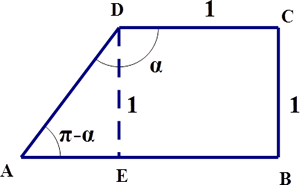
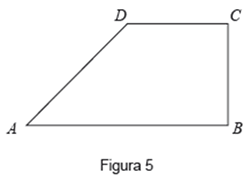
Na Figura 5, está representado um trapézio retângulo ![\left[ {ABCD} \right] \left[ {ABCD} \right]](/images/jlatex/7c39be72ce8fa6c0bf88b67de000cf8a.gif) .
.
Sabe-se que:
• 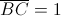
• 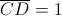
• 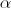 é a amplitude, em radianos, do ângulo
é a amplitude, em radianos, do ângulo 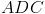
• ![\alpha \in \left] {\frac{\pi }{2},\pi } \right[ \alpha \in \left] {\frac{\pi }{2},\pi } \right[](/images/jlatex/629dd1fb1642f9bf0c494edbf9ee3d13.gif)
Resolva os itens seguintes, recorrendo a métodos exclusivamente analíticos.
1. Mostre que o perímetro do trapézio ![\left[ {ABCD} \right] \left[ {ABCD} \right]](/images/jlatex/7c39be72ce8fa6c0bf88b67de000cf8a.gif) é dado, em função de
é dado, em função de 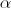 , por
, por
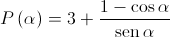 .
.
2. Para um certo número real 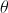 , tem-se que
, tem-se que 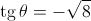 , com
, com 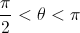 .
.
Determine o valor exato de 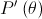 .
.
Comece por mostrar que 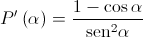 .
.