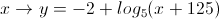Resolução do exercício de Matemática:
1.
• Interseção com o eixo dos 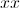 .
.
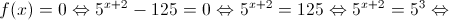
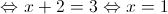
O ponto de interseção com o eixo dos 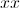 é o ponto
é o ponto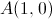
• Interseção com o eixo dos 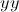 .
.
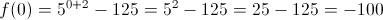
O ponto de interseção com o eixo dos 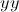 é o ponto
é o ponto 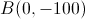
2.
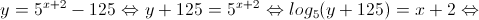
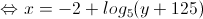
Temos que,
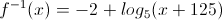
![D_{f^{-1}}=\left \{ x\in \mathbb{R}: x+125>0 \right \}=]-125;+\infty [ D_{f^{-1}}=\left \{ x\in \mathbb{R}: x+125>0 \right \}=]-125;+\infty [](/images/jlatex/e0b306ce825cf2639dc8384b6513fe5a.gif)
![f^{-1}:]-125;+\infty [\rightarrow \mathbb{R} f^{-1}:]-125;+\infty [\rightarrow \mathbb{R}](/images/jlatex/7eb1da95aa45cb0eb198bc6b59d7d85e.gif)
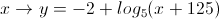
Considere a função  , definida em
, definida em 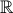 , por
, por 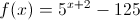 .
.
1. Determine as coordenadas dos pontos de interseção do gráfico de  com os eixos coordenados.
com os eixos coordenados.
2. Caracterize a função inversa de  .
.
Resolução do exercício de Matemática:
1.
• Interseção com o eixo dos 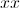 .
.
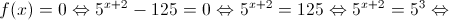
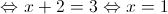
O ponto de interseção com o eixo dos 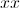 é o ponto
é o ponto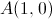
• Interseção com o eixo dos 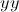 .
.
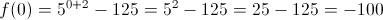
O ponto de interseção com o eixo dos 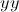 é o ponto
é o ponto 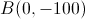
2.
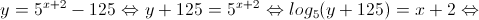
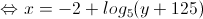
Temos que,
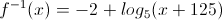
![D_{f^{-1}}=\left \{ x\in \mathbb{R}: x+125>0 \right \}=]-125;+\infty [ D_{f^{-1}}=\left \{ x\in \mathbb{R}: x+125>0 \right \}=]-125;+\infty [](/images/jlatex/e0b306ce825cf2639dc8384b6513fe5a.gif)
![f^{-1}:]-125;+\infty [\rightarrow \mathbb{R} f^{-1}:]-125;+\infty [\rightarrow \mathbb{R}](/images/jlatex/7eb1da95aa45cb0eb198bc6b59d7d85e.gif)