Resolução do exercício de matemática:
Como a reta tangente ao gráfico da função  no ponto de abcissa
no ponto de abcissa 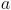 é paralela à reta de equação
é paralela à reta de equação 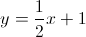 , então o seu declive é igual a
, então o seu declive é igual a  .
.
Queremos determinar 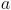 tal que
tal que 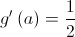 .
.
![g'\left( x \right) = {\left[ {\operatorname{sen} \left( {2x} \right) - \cos x} \right]^\prime } = 2\cos \left( {2x} \right) - \left( { - \operatorname{sen} x} \right) = 2\cos \left( {2x} \right) + \operatorname{sen} x g'\left( x \right) = {\left[ {\operatorname{sen} \left( {2x} \right) - \cos x} \right]^\prime } = 2\cos \left( {2x} \right) - \left( { - \operatorname{sen} x} \right) = 2\cos \left( {2x} \right) + \operatorname{sen} x](/images/jlatex/bf12a80952df11e0359d838e384bcbe5.gif)
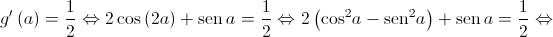
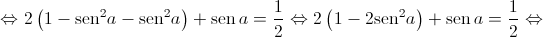
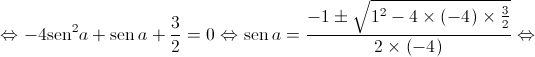
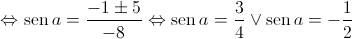
Como ![a \in \left] { - \frac{\pi }{2},0} \right[ a \in \left] { - \frac{\pi }{2},0} \right[](/images/jlatex/7294d2dfc0e18a665a3aefe0a56490eb.gif) ,
, 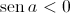 .
.
Logo, 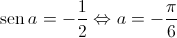 .
.
Considere a função  , de domínio
, de domínio ![\left] { - \frac{\pi }{2},0} \right[ \left] { - \frac{\pi }{2},0} \right[](/images/jlatex/8a319d3b118b0ff9d944869cbdf53ac2.gif) , definida por
, definida por 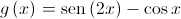 .
.
Seja 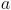 um número real do domínio de
um número real do domínio de  .
.
A reta tangente ao gráfico da função  no ponto de abcissa
no ponto de abcissa 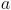 é paralela à reta de equação
é paralela à reta de equação 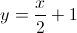 .
.
Determine o valor de 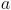 , recorrendo a métodos analíticos, sem utilizar a calculadora.
, recorrendo a métodos analíticos, sem utilizar a calculadora.
Resolução do exercício de matemática:
Como a reta tangente ao gráfico da função  no ponto de abcissa
no ponto de abcissa 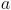 é paralela à reta de equação
é paralela à reta de equação 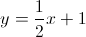 , então o seu declive é igual a
, então o seu declive é igual a  .
.
Queremos determinar 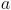 tal que
tal que 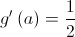 .
.
![g'\left( x \right) = {\left[ {\operatorname{sen} \left( {2x} \right) - \cos x} \right]^\prime } = 2\cos \left( {2x} \right) - \left( { - \operatorname{sen} x} \right) = 2\cos \left( {2x} \right) + \operatorname{sen} x g'\left( x \right) = {\left[ {\operatorname{sen} \left( {2x} \right) - \cos x} \right]^\prime } = 2\cos \left( {2x} \right) - \left( { - \operatorname{sen} x} \right) = 2\cos \left( {2x} \right) + \operatorname{sen} x](/images/jlatex/bf12a80952df11e0359d838e384bcbe5.gif)
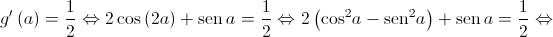
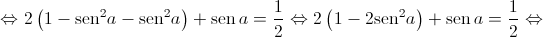
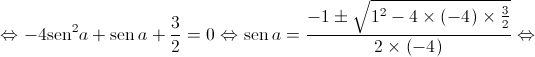
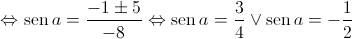
Como ![a \in \left] { - \frac{\pi }{2},0} \right[ a \in \left] { - \frac{\pi }{2},0} \right[](/images/jlatex/7294d2dfc0e18a665a3aefe0a56490eb.gif) ,
, 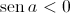 .
.
Logo, 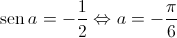 .
.