Resolução do Exercício de Matemática
1. Sendo o domínio de uma função o conjunto dos valores que podemos atribuir à variável independente 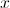 , sendo que a tangente,
, sendo que a tangente, 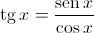 , não está definida sempre que o cosseno se anula, logo
, não está definida sempre que o cosseno se anula, logo 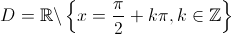 .
.
2. Para representar graficamente a função podemos utilizar o estudo efetuado no círculo trignométrico.

3. Com base na representação gráfica apresentada podemos afirmar que:
a. Periodicidade:  é uma função periódica de período positivo mínimo
é uma função periódica de período positivo mínimo 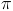 , o que significa que a função tangente assume os mesmos valores de
, o que significa que a função tangente assume os mesmos valores de 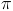 em
em 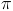 , isto é
, isto é 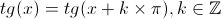

b. Zeros:  admite zeros em
admite zeros em 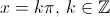
c. Extremos:  não tem extremos.
não tem extremos.
d. Paridade:  é uma função ímpar, pois
é uma função ímpar, pois 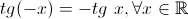 . Graficamente esta propriedade traduz-se pela existência de simetria relativamente à origem do referencial.
. Graficamente esta propriedade traduz-se pela existência de simetria relativamente à origem do referencial.
e. Injetividade:  não é injetiva, pois é uma função periódica, isto é, há inúmeros objetos diferentes que têm a mesma imagem, exemplo
não é injetiva, pois é uma função periódica, isto é, há inúmeros objetos diferentes que têm a mesma imagem, exemplo 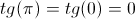
f. Contradomínio: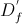
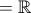

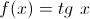 .
.



