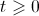A Figura 2 representa parte da tabela publicada pelo Instituto Hidrográfico com as previsões das alturas de maré, no porto de Leixões, para os sete primeiros dias do mês de julho de 2010.
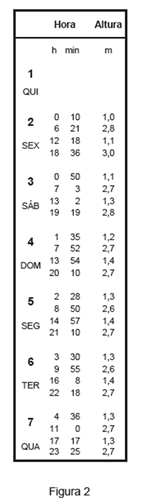
Os valores das alturas estão em metros e o tempo é indicado em horas e minutos de cada dia.
Com base nos dados da tabela publicada pelo Instituto Hidrográfico, o Rui obteve, por regressão sinusoidal, a seguinte expressão, que relaciona a altura de maré, M, em metros, no porto de Leixões, com o tempo, t, em horas, contado a partir das zero horas do dia 1 de julho de 2010:
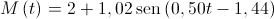 para
para 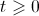
O argumento da função seno está em radianos.
1.1. Descreva, com base na expressão obtida pelo Rui, a previsão da variação da altura de maré durante o primeiro dia de
julho de 2010, indicando os instantes entre os quais a maré subiria e os instantes entre os quais a maré desceria.
Apresente os valores em horas e minutos, com os minutos arredondados às unidades.
Em cálculos intermédios, utilize valores arredondados às centésimas.
1.2. Determine a diferença entre a altura de maré prevista pelo Instituto Hidrográfico para as 18 horas e 36 minutos do
dia 2 de julho de 2010 e a altura de maré, para o mesmo instante, dada pela expressão obtida pelo Rui.
Apresente o resultado em metros, arredondado às décimas.
Se, em cálculos intermédios, proceder a arredondamentos, conserve pelo menos três casas decimais.
Resolução do exercício de matemática:
1.1.

6,02 horas ? 06h 01min
12,30 horas ? 12h 18min
18,59 horas ? 18h 35min
Desde as zero horas até às 6 horas e 1 minuto a maré esteve a subir.
Depois deste instante e até às 12 horas e 18 minutos a maré esteve a descer.
Desde este instante e até às 18 horas e 35 minutos a maré voltou a subir.
A partir deste instante e até ao fim do dia, a maré esteve a descer.
1.2.
18h 36min ? 18,6 horas
24 + 18,6 = 42,6
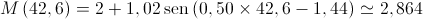
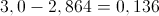
Logo, a diferença é de 0,1 metros.

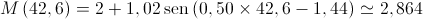
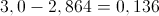


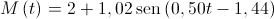 para
para