Exame Nacional de Matemática B 2ª Fase 2011 - Grupo 4
Numa determinada região, existe um lago natural onde foram efetuadas descargas de resíduos poluentes.
Uma associação ambientalista detetou que a concentração, na água desse lago, de uma determinada substância poluente era muito elevada, o que punha em risco a sobrevivência de algumas espécies aí existentes, entre as quais a truta.
1. No início do ano de 1995, começaram a ser implementadas diversas medidas para diminuir a concentração da substância poluente e, assim, melhorar a qualidade da água desse lago.
Admita que a concentração da substância poluente, , em miligramas por metro cúbico de água, anos após o início do ano de 1995, é dada por
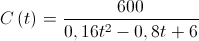 para
para 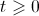
1.1 Determine o ano em que a concentração da substância poluente existente na água do lago ficou reduzida a metade do seu valor inicial.
1.2 Existe um único instante em que a taxa de variação instantânea da função 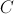 muda de sinal, passando de positiva a negativa. Interprete, no contexto do problema, o significado desse instante.
muda de sinal, passando de positiva a negativa. Interprete, no contexto do problema, o significado desse instante.
2. O número de trutas existentes no lago diminuiu acentuadamente em consequência das descargas de resíduos poluentes. Alguns anos depois de as descargas terem ocorrido, procedeu-se ao repovoamento do lago com exemplares desta espécie.
Admita queo número de trutas existentes no lago, 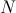 , em milhares,
, em milhares, 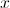 semanas após o início do repovoamento, é dado, aproximadamente, por
semanas após o início do repovoamento, é dado, aproximadamente, por
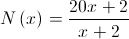 para
para 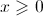
2.1 Mostre que, de acordo com o modelo apresentado, entre a segunda e a oitava semanas, se registou um aumento médio de 950 trutas, por semana.
2.2 O número de trutas existentes no lago, imediatamente antes de ocorrerem as descargas de resíduos poluentes, foi estimado em 22 000. Averigue se, de acordo com o modelo apresentado, o número de trutas no lago poderá vir a atingir o valor que foi estimado para a população de trutas existentes no lago imediatamente antes de ocorrerem as referidas descargas. Justifique a sua resposta, usando propriedades da função 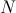 .
.
3. Perto do lago, existe um sistema integrado de vários aquários. Em cada um dos aquários do sistema, vivem, em equilíbrio, diferentes espécies aquáticas.
A equipa de biólogos responsável pelo sistema tem como objetivo a preservação e o estudo dessas espécies, e utiliza o conceito de diversidade biológica.
Admita que a diversidade biológica, 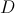 , de um ecossistema, no qual vivem
, de um ecossistema, no qual vivem 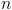 espécies com igual número de efetivos, é dada por
espécies com igual número de efetivos, é dada por 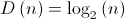 , sendo
, sendo 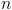 um número inteiro positivo.
um número inteiro positivo.
Num aquário, os biólogos pretendem colocar 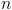 espécies diferentes com igual número de efetivos.
espécies diferentes com igual número de efetivos.
Determine, de acordo com as condições referidas, o número mínimo de espécies que é necessário colocar no aquário, de modo que a diversidade nesse aquário não seja inferior a 4,3.
Exame Nacional de Matemática B 2ª Fase 2011 - Grupo 4→

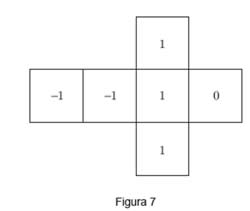
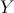 , que representa o «produto dos números saídos em dois lançamentos de dado cúbico».
, que representa o «produto dos números saídos em dois lançamentos de dado cúbico».
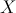 , «altura, em centímetros, de um aluno da Escola Secundária Boavista, escolhido ao acaso».
, «altura, em centímetros, de um aluno da Escola Secundária Boavista, escolhido ao acaso».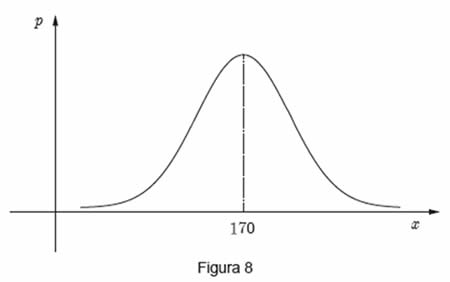
![\left[ {AB} \right] \left[ {AB} \right]](/images/jlatex/103109231bf469cee07093a66be902fa.gif) , constroem-se dois quadrados geometricamente iguais,
, constroem-se dois quadrados geometricamente iguais, ![\left[ {ACED} \right] \left[ {ACED} \right]](/images/jlatex/6cb7960befaf09afe0844db59b17b1cb.gif) e
e ![\left[ {CBFE} \right] \left[ {CBFE} \right]](/images/jlatex/c3ab7302ae8bc318cd2c200d8e0ebfcc.gif) , obtendo-se a linha 1 de quadrados.
, obtendo-se a linha 1 de quadrados.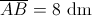
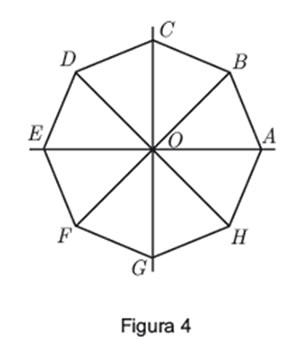
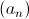 , cujo termo de ordem
, cujo termo de ordem ![\left[ {ABCDEFGH} \right] \left[ {ABCDEFGH} \right]](/images/jlatex/6c587cd222f453012dfd43a1171f5cd7.gif) , com centro no ponto
, com centro no ponto 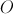 , os segmentos de reta
, os segmentos de reta ![\left[ {FB} \right] \left[ {FB} \right]](/images/jlatex/4d2a6c7fbf05a9613b06ca886da6776a.gif) e
e ![\left[ {DH} \right] \left[ {DH} \right]](/images/jlatex/36c233ebd45dc8eb11755cd7c9ed1fef.gif) e as retas
e as retas 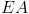 e
e 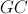 .
.
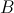 no ponto
no ponto 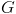 .
.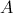 e
e 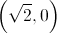 .
.
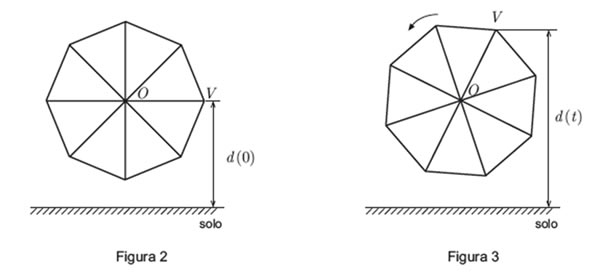
![\left[ {OV} \right] \left[ {OV} \right]](/images/jlatex/96e3fd59811e435d67fb9a18c28fc0e5.gif) estava posicionada paralelamente ao solo, como sugere a Figura 2;
estava posicionada paralelamente ao solo, como sugere a Figura 2;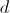 , em metros, do ponto
, em metros, do ponto  ao solo,
ao solo,  segundos após as velas terem começado a rodar, é dada, durante o intervalo de tempo em que as velas rodaram, por
segundos após as velas terem começado a rodar, é dada, durante o intervalo de tempo em que as velas rodaram, por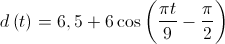 para
para ![t \in \left[ {0,900} \right] t \in \left[ {0,900} \right]](/images/jlatex/73d781ff320b01e11a1b67de7a07a0f4.gif)