Exercicios de Matematica 12 ANO - Derivadas - Exercício 2
Seja  uma função cuja derivada
uma função cuja derivada 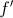 , de domínio
, de domínio 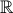 , é dada por
, é dada por 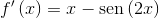 .
.
6.1. Determine o valor de 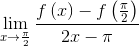 .
.
6.2. Estude o gráfico da função  , quanto ao sentido das concavidades e quanto à existência de pontos de inflexão em
, quanto ao sentido das concavidades e quanto à existência de pontos de inflexão em
![\left] { - \frac{\pi }{2},\frac{\pi }{4}} \right[ \left] { - \frac{\pi }{2},\frac{\pi }{4}} \right[](/images/jlatex/3b07aac6fc2936bf16463b2b571027aa.gif) , recorrendo a métodos analíticos, sem utilizar a calculadora.
, recorrendo a métodos analíticos, sem utilizar a calculadora.
Na sua resposta, deve indicar o(s) intervalo(s) onde o gráfico da função  tem concavidade voltada para cima,
tem concavidade voltada para cima,
o(s) intervalo(s) onde o gráfico da função  tem concavidade voltada para baixo e, caso existam, as abcissas
tem concavidade voltada para baixo e, caso existam, as abcissas
dos pontos de inflexão do gráfico da função  .
.

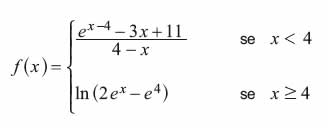
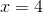 .
.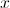 tende para
tende para 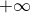 , de equação
, de equação 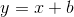 , com
, com 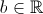 .
.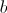 .
. , de domínio
, de domínio ![\left] {0, + \infty } \right[ \left] {0, + \infty } \right[](/images/jlatex/2631d35d1244d95aa0e498635fa2d286.gif) , definidas por:
, definidas por: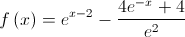 e
e 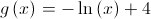
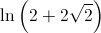 é o único zero da função
é o único zero da função  , os gráficos das funções
, os gráficos das funções ![\left[ {OAB} \right] \left[ {OAB} \right]](/images/jlatex/4985071c7575856642f0b0d086715c52.gif) .
. é a origem do referencial;
é a origem do referencial;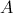 e
e 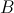 são pontos do gráfico de
são pontos do gráfico de 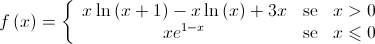
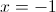 .
.