Resolução do Exercício:
A resposta correta é a (A).
Explicação:
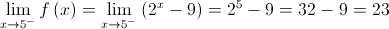
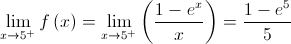
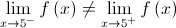
Logo, não existe 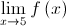 .
.
Logo  é descontínua no ponto de abcissa 5.
é descontínua no ponto de abcissa 5.
Logo, o intervalo escolhido não pode conter o 5.
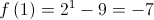
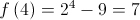
Como  é contínua em
é contínua em ![\left[ {1,4} \right] \left[ {1,4} \right]](/images/jlatex/ffa8463a138c1d01d5fde16900d9e6c6.gif) e
e 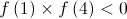 , então
, então  pelo Teorema de Bolzano tem pelo menos um zero em
pelo Teorema de Bolzano tem pelo menos um zero em![\left] {1,4} \right[ \left] {1,4} \right[](/images/jlatex/f2e09f26592828145a7fb3609035a8b0.gif) .
.

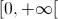 , definida por:
, definida por: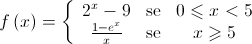
![\left] {0,1} \right[ \left] {0,1} \right[](/images/jlatex/3f310af7ae64b30edb352537f24808b4.gif)
![\left] {4,6} \right[ \left] {4,6} \right[](/images/jlatex/ced08cb5c2687456b084c0ae272cc71f.gif)
![\left] {6,7} \right[ \left] {6,7} \right[](/images/jlatex/b438c177bea9775a37494f059c2f6554.gif)




