Resolução do exercício de matemática:
1.
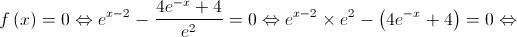
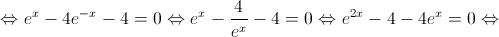
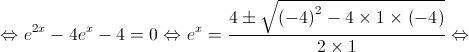
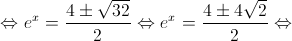
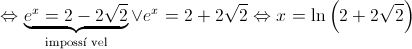
2.
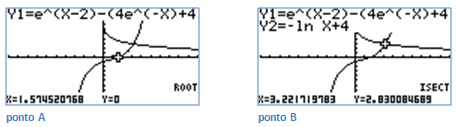
A abcissa do ponto A é 1,57.
B(3,22 ; 2,83)
![{A_{\left[ {OAB} \right]}} = \frac{{1,57 \times 2,83}}{2} \approx 2,2 {A_{\left[ {OAB} \right]}} = \frac{{1,57 \times 2,83}}{2} \approx 2,2](/images/jlatex/aa96fed67d8797a43294554ad882f52f.gif)
A área do triângulo é de 2,2 u.a. aproximadamente.
Considere a função  , de domínio
, de domínio 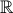 , e a função
, e a função  , de domínio
, de domínio ![\left] {0, + \infty } \right[ \left] {0, + \infty } \right[](/images/jlatex/2631d35d1244d95aa0e498635fa2d286.gif) , definidas por:
, definidas por:
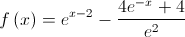 e
e 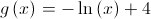
1. Mostre que 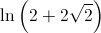 é o único zero da função
é o único zero da função  , recorrendo a métodos
, recorrendo a métodos
exclusivamente analíticos.
2. Considere, num referencial o.n. 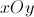 , os gráficos das funções
, os gráficos das funções  e
e  e o triângulo
e o triângulo ![\left[ {OAB} \right] \left[ {OAB} \right]](/images/jlatex/4985071c7575856642f0b0d086715c52.gif) .
.
Sabe-se que:
•  é a origem do referencial;
é a origem do referencial;
• 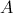 e
e 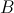 são pontos do gráfico de
são pontos do gráfico de  ;
;
• a abcissa do ponto 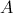 é o zero da função
é o zero da função  ;
;
• o ponto 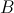 é o ponto de interseção do gráfico da função
é o ponto de interseção do gráfico da função  com o gráfico da função
com o gráfico da função  .
.
Determine a área do triângulo ![\left[ {OAB} \right] \left[ {OAB} \right]](/images/jlatex/4985071c7575856642f0b0d086715c52.gif) , recorrendo à calculadora gráfica.
, recorrendo à calculadora gráfica.
Na sua resposta, deve:
• reproduzir os gráficos das funções  e
e  , devidamente identificado(s), incluindo o referencial;
, devidamente identificado(s), incluindo o referencial;
• assinalar os pontos 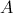 e
e 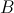 ;
;
• indicar a abcissa do ponto 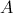 e as coordenadas do ponto
e as coordenadas do ponto 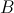 com arredondamento às centésimas;
com arredondamento às centésimas;
• apresentar o valor da área pedida com arredondamento às décimas.
Resolução do exercício de matemática:
1.
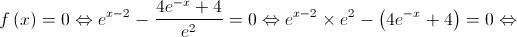
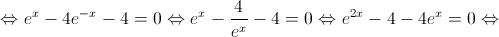
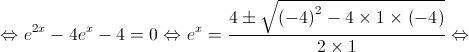
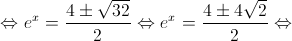
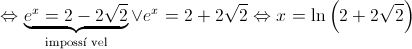
2.

A abcissa do ponto A é 1,57.
B(3,22 ; 2,83)
![{A_{\left[ {OAB} \right]}} = \frac{{1,57 \times 2,83}}{2} \approx 2,2 {A_{\left[ {OAB} \right]}} = \frac{{1,57 \times 2,83}}{2} \approx 2,2](/images/jlatex/aa96fed67d8797a43294554ad882f52f.gif)
A área do triângulo é de 2,2 u.a. aproximadamente.