Resolução do exercício de matemática:
![g''\left( x \right) = {\left[ {\ln \left( {{e^x} + 6{e^{ - x}} + 4x} \right)} \right]^\prime } = \frac{{{{\left( {{e^x} + 6{e^{ - x}} + 4x} \right)}^\prime }}}{{{e^x} + 6{e^{ - x}} + 4x}} = \frac{{{e^x} - 6{e^{ - x}} + 4}}{{{e^x} + 6{e^{ - x}} + 4x}} g''\left( x \right) = {\left[ {\ln \left( {{e^x} + 6{e^{ - x}} + 4x} \right)} \right]^\prime } = \frac{{{{\left( {{e^x} + 6{e^{ - x}} + 4x} \right)}^\prime }}}{{{e^x} + 6{e^{ - x}} + 4x}} = \frac{{{e^x} - 6{e^{ - x}} + 4}}{{{e^x} + 6{e^{ - x}} + 4x}}](/images/jlatex/56a1fc95d6193c134587aa1aa22ab3b8.gif)
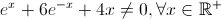
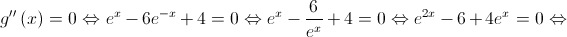
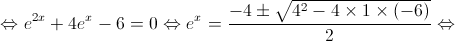
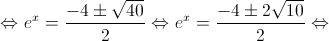
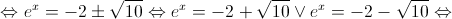
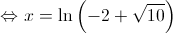
Nota: a equação 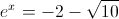 é impossível uma vez que
é impossível uma vez que 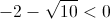 .
.

O gráfico de  tem a concavidade voltada para baixo no intervalo
tem a concavidade voltada para baixo no intervalo ![\left] {0,{\text{ }}\ln \left( { - 2 + \sqrt {10} } \right)} \right] \left] {0,{\text{ }}\ln \left( { - 2 + \sqrt {10} } \right)} \right]](/images/jlatex/650ccaa97204147253085bdd8c007810.gif) e voltada para cima em
e voltada para cima em 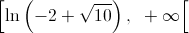 .
.
O gráfico de  tem um ponto de inflexão de abcissa
tem um ponto de inflexão de abcissa 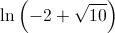 .
.
Seja  uma função, de domínio
uma função, de domínio 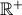 , cuja derivada,
, cuja derivada, 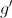 , de domínio
, de domínio 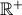 , é dada por
, é dada por
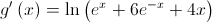
Estude a função  quanto ao sentido das concavidades do gráfico e quanto à existência de pontos de inflexão, recorrendo a métodos analíticos, sem utilizar a calculadora.
quanto ao sentido das concavidades do gráfico e quanto à existência de pontos de inflexão, recorrendo a métodos analíticos, sem utilizar a calculadora.
Resolução do exercício de matemática:
![g''\left( x \right) = {\left[ {\ln \left( {{e^x} + 6{e^{ - x}} + 4x} \right)} \right]^\prime } = \frac{{{{\left( {{e^x} + 6{e^{ - x}} + 4x} \right)}^\prime }}}{{{e^x} + 6{e^{ - x}} + 4x}} = \frac{{{e^x} - 6{e^{ - x}} + 4}}{{{e^x} + 6{e^{ - x}} + 4x}} g''\left( x \right) = {\left[ {\ln \left( {{e^x} + 6{e^{ - x}} + 4x} \right)} \right]^\prime } = \frac{{{{\left( {{e^x} + 6{e^{ - x}} + 4x} \right)}^\prime }}}{{{e^x} + 6{e^{ - x}} + 4x}} = \frac{{{e^x} - 6{e^{ - x}} + 4}}{{{e^x} + 6{e^{ - x}} + 4x}}](/images/jlatex/56a1fc95d6193c134587aa1aa22ab3b8.gif)
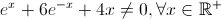
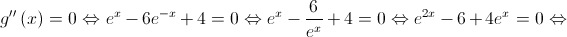
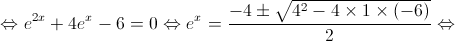
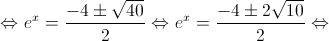
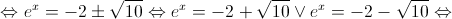
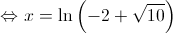
Nota: a equação 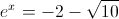 é impossível uma vez que
é impossível uma vez que 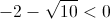 .
.

O gráfico de  tem a concavidade voltada para baixo no intervalo
tem a concavidade voltada para baixo no intervalo ![\left] {0,{\text{ }}\ln \left( { - 2 + \sqrt {10} } \right)} \right] \left] {0,{\text{ }}\ln \left( { - 2 + \sqrt {10} } \right)} \right]](/images/jlatex/650ccaa97204147253085bdd8c007810.gif) e voltada para cima em
e voltada para cima em 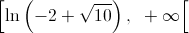 .
.
O gráfico de  tem um ponto de inflexão de abcissa
tem um ponto de inflexão de abcissa 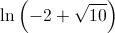 .
.