Em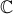 , conjunto dos números complexos, considere
, conjunto dos números complexos, considere
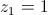 ,
,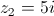 e
e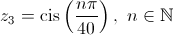
Resolva os dois itens seguintes sem recorrer à calculadora.
1.
O complexo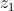 é raiz do polinómio
é raiz do polinómio .
.
Determine, em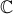 , as restantes raízes do polinómio.
, as restantes raízes do polinómio.
Apresente as raízes obtidas na forma trigonométrica.
2.
Determine o menor valor de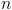 natural para o qual a imagem geométrica de
natural para o qual a imagem geométrica de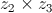 , no plano complexo, está no terceiro quadrante e pertence à bissetriz dos quadrantes ímpares.
, no plano complexo, está no terceiro quadrante e pertence à bissetriz dos quadrantes ímpares.
Resolução do Exercício:
1.
Utizando a regra de Ruffini para dividir por
por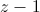 , tem-se:
, tem-se:
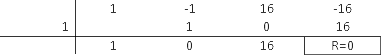
Logo: 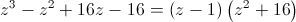
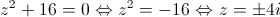
Logo, as raízes do polinómio na forma trigonométrica são:
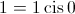 ;
; 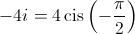 e
e 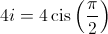
2.
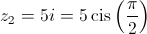
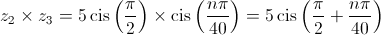
Como a imagem geométrica de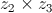 , no plano complexo, está no terceiro quadrante e pertence à bissetriz dos quadrantes ímpares tem-se que ter:
, no plano complexo, está no terceiro quadrante e pertence à bissetriz dos quadrantes ímpares tem-se que ter:
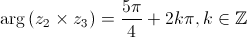
Isto é,
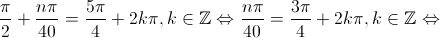
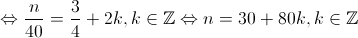
O menor natural que satisfaz a condição anterior é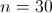 (corresponde a
(corresponde a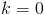 ).
).
 por
por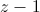 , tem-se:
, tem-se: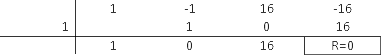
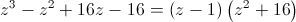
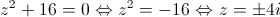
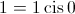 ;
; 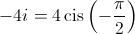 e
e 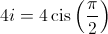
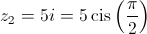
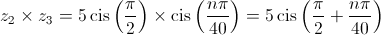
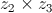 , no plano complexo, está no terceiro quadrante e pertence à bissetriz dos quadrantes ímpares tem-se que ter:
, no plano complexo, está no terceiro quadrante e pertence à bissetriz dos quadrantes ímpares tem-se que ter: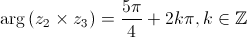
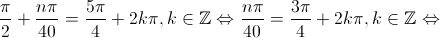
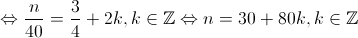
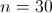 (corresponde a
(corresponde a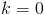 ).
).
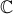 , conjunto dos números complexos, considere
, conjunto dos números complexos, considere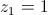 ,
,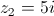 e
e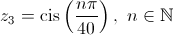
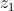 é raiz do polinómio
é raiz do polinómio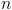 natural para o qual a imagem geométrica de
natural para o qual a imagem geométrica de



