Resolução do exercício de matemática:
Considere-se a função  , definida por
, definida por 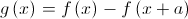 .
.
Tem-se que: 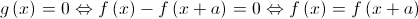
A função  é contínua em
é contínua em ![\left[ { - a,0} \right] \left[ { - a,0} \right]](/images/jlatex/50064968830937f6d9fbe2801713f0d9.gif) porque é a diferença de duas funções contínuas nesse intervalo.
porque é a diferença de duas funções contínuas nesse intervalo.
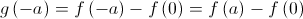
![g\left( 0 \right) = f\left( 0 \right) - f\left( a \right) = - f\left( a \right) + f\left( 0 \right) = - \left[ {f\left( a \right) - f\left( 0 \right)} \right] g\left( 0 \right) = f\left( 0 \right) - f\left( a \right) = - f\left( a \right) + f\left( 0 \right) = - \left[ {f\left( a \right) - f\left( 0 \right)} \right]](/images/jlatex/aec1e7d45bcdd6853cec5a3ac1f75e90.gif)
Tem-se que:
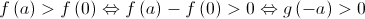
![g\left( 0 \right) = - \left[ {f\left( a \right) - f\left( 0 \right)} \right] < 0 g\left( 0 \right) = - \left[ {f\left( a \right) - f\left( 0 \right)} \right] < 0](/images/jlatex/4319dfea1fcbc1341873db37ea330381.gif)
Logo, 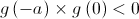 .
.
Como  é contínua em
é contínua em ![\left[ { - a,0} \right] \left[ { - a,0} \right]](/images/jlatex/50064968830937f6d9fbe2801713f0d9.gif) e
e 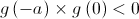 , pelo Teorema de Bolzano, existe pelo menos um zero da função no intervalo
, pelo Teorema de Bolzano, existe pelo menos um zero da função no intervalo ![\left] { - a,0} \right[ \left] { - a,0} \right[](/images/jlatex/c6c78f699a4b8bc661c121630153e0b9.gif) .
.
Logo, a condição 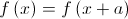 tem, pelo menos, uma solução em
tem, pelo menos, uma solução em ![\left] { - a,0} \right[ \left] { - a,0} \right[](/images/jlatex/c6c78f699a4b8bc661c121630153e0b9.gif) .
.

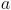 positivo, uma função
positivo, uma função  , contínua, de domínio
, contínua, de domínio ![\left[ { - a,a} \right] \left[ { - a,a} \right]](/images/jlatex/8f7789c40e13a9d56fc3916d7d539b99.gif) .
.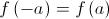 e
e 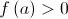 .
.



