Resolução do Exercício
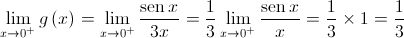
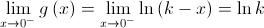
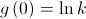
Como  é contínua em
é contínua em 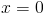 , então:
, então:
![\ln k = \frac{1}{3} \Leftrightarrow k = {e^{\frac{1}{3}}} \Leftrightarrow k = \sqrt[3]{e} \ln k = \frac{1}{3} \Leftrightarrow k = {e^{\frac{1}{3}}} \Leftrightarrow k = \sqrt[3]{e}](/images/jlatex/5e796d2d68ba1abc38797ab06e6fccd9.gif)
Opção correta: (A)
Para um certo número real positivo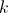 , a função
, a função  definida em
definida em 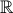 por:
por:
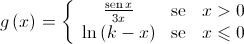
é contínua.
Qual é o valor de 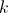 ?
?
(A) ![\sqrt[3]{e} \sqrt[3]{e}](/images/jlatex/fbf1ec86e8fd79251b9fa5725d7b74d7.gif)
(B) 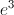
(C) 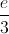
(D) 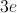
Resolução do Exercício
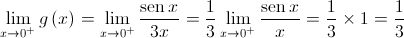
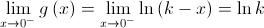
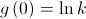
Como  é contínua em
é contínua em 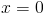 , então:
, então:
![\ln k = \frac{1}{3} \Leftrightarrow k = {e^{\frac{1}{3}}} \Leftrightarrow k = \sqrt[3]{e} \ln k = \frac{1}{3} \Leftrightarrow k = {e^{\frac{1}{3}}} \Leftrightarrow k = \sqrt[3]{e}](/images/jlatex/5e796d2d68ba1abc38797ab06e6fccd9.gif)
Opção correta: (A)