Resolução do Exercício
1.
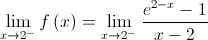
Fazendo 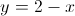 temos que quando
temos que quando 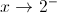 vem
vem  ; logo:
; logo:
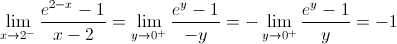
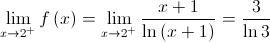
Logo, não existem assíntotas verticais.
2.
A função  é contínua em
é contínua em 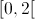 porque é o quociente de funções contínuas; logo é contínua no intervalo
porque é o quociente de funções contínuas; logo é contínua no intervalo ![\left[ {0,\frac{1}{2}} \right] \left[ {0,\frac{1}{2}} \right]](/images/jlatex/2060bfc1e0b719ad4915e1b7608f8fde.gif) .
.

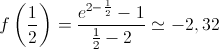
Como é contínua em ![\left[ {0,\frac{1}{2}} \right] \left[ {0,\frac{1}{2}} \right]](/images/jlatex/2060bfc1e0b719ad4915e1b7608f8fde.gif) e
e 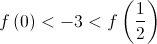 , então, pelo teorema de Bolzano, existe pelo menos um valor de
, então, pelo teorema de Bolzano, existe pelo menos um valor de 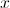 pertencente a
pertencente a 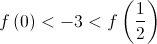 tal que
tal que 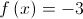 .
.
3.
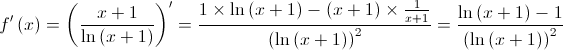
Para 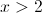 , temos que
, temos que 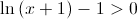 , e, por outro lado,
, e, por outro lado, 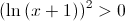 pelo que:
pelo que: ![f'\left( x \right) > 0,\forall x \in \left] {2, + \infty } \right[ f'\left( x \right) > 0,\forall x \in \left] {2, + \infty } \right[](/images/jlatex/a213215ca92b759b79745ee60f770124.gif) .
.
Logo,  é estritamente crescente em
é estritamente crescente em ![\left] {2, + \infty } \right[ \left] {2, + \infty } \right[](/images/jlatex/aba2e90d9254a962a10b0d0dbae4eefa.gif) .
.

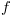 , de domínio
, de domínio 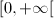 , definida por
, definida por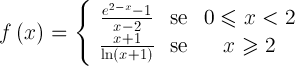
![\left] {0,\frac{1}{2}} \right[ \left] {0,\frac{1}{2}} \right[](/images/jlatex/3a22da03bfe5e59c313c4ed2e8900ff7.gif) .
.



