Resolução do exercício de matemática:
4.1.  é contínua em
é contínua em 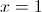 se e só se
se e só se 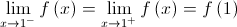 .
.
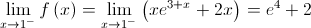
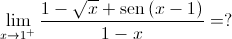
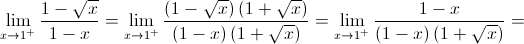
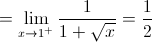
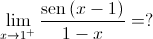
Mudança de variável: 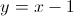 (quando
(quando 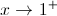 , então
, então  )
)
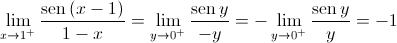
Logo, 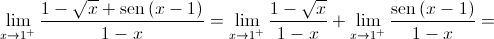
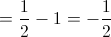
Logo,  não é contínua em
não é contínua em 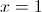 .
.
4.2. 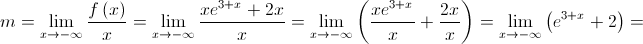
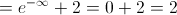
![b = \mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - 2x} \right] = \mathop {\lim }\limits_{x \to - \infty } \left( {x{e^{3 + x}} + 2x - 2x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {x{e^{3 + x}}} \right) b = \mathop {\lim }\limits_{x \to - \infty } \left[ {f\left( x \right) - 2x} \right] = \mathop {\lim }\limits_{x \to - \infty } \left( {x{e^{3 + x}} + 2x - 2x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {x{e^{3 + x}}} \right)](/images/jlatex/ab86ea33ef3356c4995333ed27a459fb.gif)
Mudança de variável: 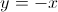 (quando
(quando 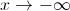 , então
, então  )
)
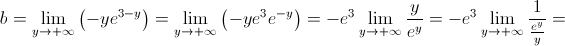
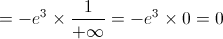
O gráfico de  admite uma assíntota oblíqua de equação
admite uma assíntota oblíqua de equação 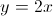 , quando
, quando 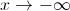 .
.

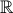 , definida por:
, definida por: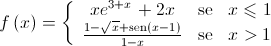
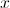 tende para
tende para 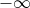 .
.



