Resolução do exercício de matemática:
1.
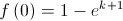
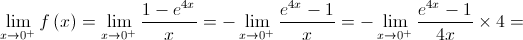
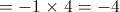
(quando 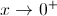 ,
, 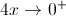 ).
).
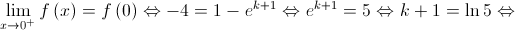
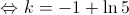
2.
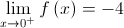

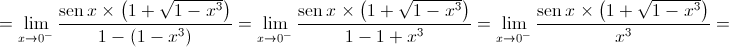
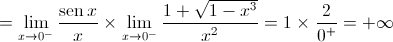
Logo, 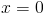 é a única assíntota vertical do gráfico da função
é a única assíntota vertical do gráfico da função  uma vez que esta é contínua em
uma vez que esta é contínua em 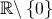 .
.
3.
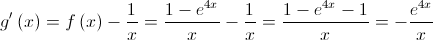
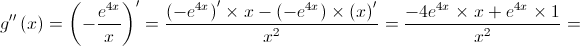
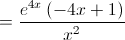
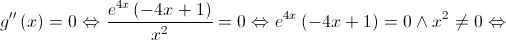
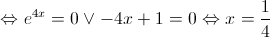
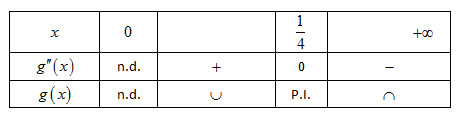
A função  tem um ponto de inflexão de abcissa
tem um ponto de inflexão de abcissa  ;
;
Concavidade voltada para cima em ![\left] {0,\frac{1}{4}} \right[ \left] {0,\frac{1}{4}} \right[](/images/jlatex/d58b3da6d6fc835d7944a7cb12f05257.gif) ;
;
Concavidade voltada para baixo em ![\left] {\frac{1}{4}, + \infty } \right[ \left] {\frac{1}{4}, + \infty } \right[](/images/jlatex/c95c355802a0a3da818acb0a4ba9157d.gif) .
.

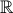 , definida por:
, definida por: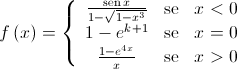
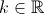 .
.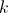 , de modo que
, de modo que 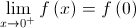 .
.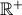 , cuja derivada
, cuja derivada 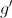 , de domínio
, de domínio 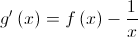 .
.



